Curva logística e curva exponencial

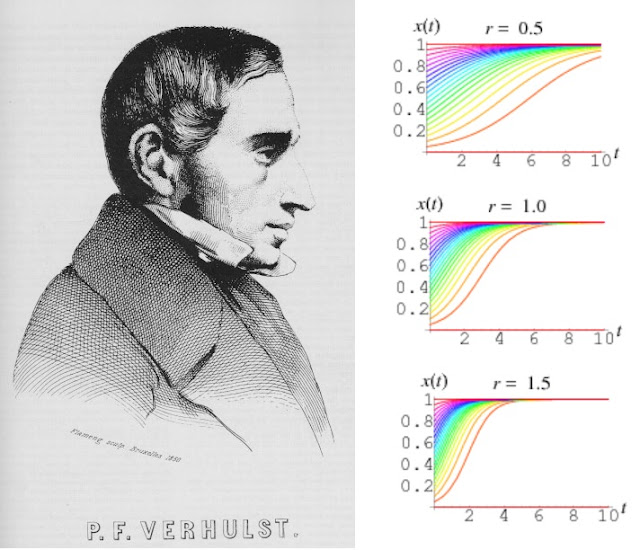
Com a pandemia do coronavírus atacando em escala global, temos que limitar nossa mobilidade sob pena de acelerar ainda mais o avanço do número de casos na população. Sem a diminuição da mobilidade o crescimento no número de doentes seria exponencial e o sistema de saúde não teria como dar conta. O número de mortos seria imenso aqui no Brasil (ou no mundo). Isso ocorre porque uma pessoa infectada pode transmitir o vírus mesmo estando assintomática, podendo contaminar várias pessoas, em poucos dias essas novas pessoas contaminadas passam a contaminas outras, e assim por diante. Isso causa o crescimento exponencial no número de casos, na verdade é um crescimento logístico. Existe uma diferença nem um pouco sutil entre eles: o crescimento exponencial, em princípio, não tem limite (pode ir ao infinito); já o crescimento logístico tem início semelhante a uma curva exponencial, mas é limitado a valor máximo e antes de atingir esse máximo a curva começa a crescer mais lentamente. Não se pode infectar mais pessoas do que o total da população, daí a limitação no máximo de infectados e a "transformação" da curva exponencial em uma curva logística. Aparentemente, foi Pierre-François Verhulst (1804–1849) o primeiro a encontrar essa curva quando estava estudando o crescimento populacional auto limitante. Existem várias outras aplicações em que a curva logística pode ser usada como modelo (ver aqui).

Matematicamente, as curvas exponencial e logísticas são as soluções das equações

\[ \frac{dx}{dt} = K_a x_e\]
\[ \frac{dx}{dt} = K_a x_l (K_b - x_l) ,\]

a curva logística pode crescer até $K_b$. Sendo $K_a$ e $K_b$ valores positivos, as curvas serão sempre crescentes. As soluções são:

\[ x_e(t) = x_0 e^{K_a t}\]
\[ x_l(t) = \frac{K_B}{1 + K e^{-K_A K_B t}}\]

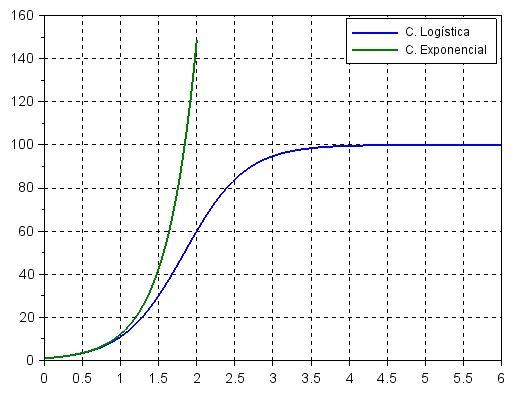
Onde $x_0$ e $K_B/K$ são os valores iniciais em $t = 0$. Para mais informações matemática, ver aqui. O exemplo abaixo mostra uma comparação entre as curvas exponencial e logística, notar o início coincidente.

Código Scilab:

clc; xdel(winsid());
kb = 100.0;
ka = 0.025;
t=0:0.01:6;
kc = kb - 1;
y = kb./(1+kc*exp(-ka*kb*t));
t2 = 0:0.01:2;
y2 = exp(ka*kb*t2);
plot(t,y,t2,y2);
legend('C. Logística','C. Exponencial');
title('Exemplos de curva logística e exponencial');
xgrid;