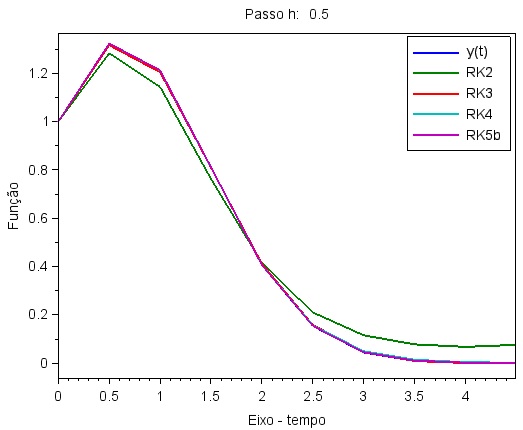
 |
| Uso de um passo muito grande para solução de uma EDO, o método RK-2 apresenta um erro significativo. |
Em muitas situações, o método de Runge-Kutta (RK) de 4a. ordem tem precisão suficiente para resolver numericamente uma EDO (equação diferencial ordinária) - ver postagens antigas aqui neste mesmo
blog (
aqui) - de forma satisfatória. Entretanto, se for necessária uma maior precisão, podemos tentar um método RK de ordem mais elevada. Em casos extremos, um método ordem Runge-Kutta-Nyström ( RKN1210 12a./10a.) pode ser tentado. Nessa postagem, apresentamos uma comparação entre os métodos RK de ordem 2, 3, 4 (forma clássica) e 5 (método sugerido por Butcher - ver aqui a página desse pesquisador
aqui). Existem várias fórmulas possíveis para esses métodos, aqui apresentamos as mais comuns. São elas:
RK-2:
\begin{align*}
K_1 & = hf(t_k,y(t_k)) \\
K_2 & = hf(t_k + h,y(t_k) + K_1) \\
y(t_{k+1}) & = y(t_k) + \frac{K_1+K_2}{2}\\
t_{k+1} & = t_k + h
\end{align*}
RK-3:
\begin{align*}
K_1 & = hf(t_k,y_k) \\
K_2 & = hf(t_k + h/2,y_k + K_1/2) \\
K_3 & = hf(t_k + h,y_k + K_2) \\
y_{k+1} & = y_{k} + \frac{1}{4}(K_1 + 2K_2 + K_3)\\
t_{k+1} & = t_k + h
\end{align*}
RK-4:
\begin{align*}
K_1 & = hf(t_k,y_k) \\
K_2 & = hf(t_k + h/2,y_k + K_1/2) \\
K_3 & = hf(t_k + h/2,y_k + K_2/2) \\
K_4 & = hf(t_k + h,y_k + K_3) \\
y_{k+1} & = y_{k} + \frac{1}{6}(K_1 + 2K_2 + 2K_3 + K_4) \\
t_{k+1} & = t_k + h
\end{align*}
RK-5:
\begin{align*}
K_1 &= h f(t_k,y_k);\\
K_2 &= h f(t_k+h/4,y_k+K_1/4);\\
K_3 &= h f(t_k+h/4,y_k+(K_1+K_2)/8);\\
K_4 &= h f(t_k+h/2,y_k+(K_3 - K_2/2));\\
K_5 &= h f(t_k+3*h/4,y_k+(3 K_1 + 9 K_4)/16); \\
K_6 &= h f(t_k+h,y5kb+(-3 K_1+2 K_2+12 K_3 - 12 K_4 + 8 K_5)/7); \\
y_{k+1} &= y_k + (7 K_1 + 32 K_3 + 12 K_4 + 32 K_5 + 7 K_6)/90;
\end{align*}
Iremos testar a EDO:
\begin{equation*}
\frac{dy}{dx} = \exp(-x^2/2) - yx;
\end{equation*}
cuja solução analítica é
\begin{equation*}
y = (x+1)\exp(-x^2/2);
\end{equation*}
usando os métodos RK descritos acima. Para saber mais sobre os métodos RK para solução de EDOs ver
aqui e
aqui.
Gráficos:
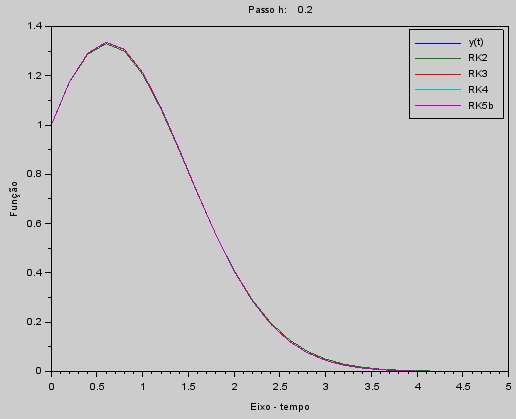 |
| Comparação da solução analítica com as soluções numéricas. |
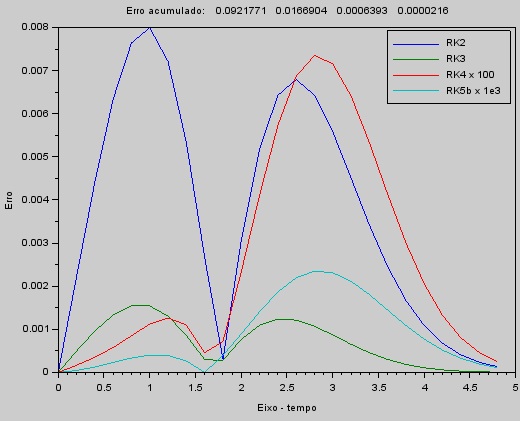 |
| Menor erro para os métodos RK de ordem mais alta. |
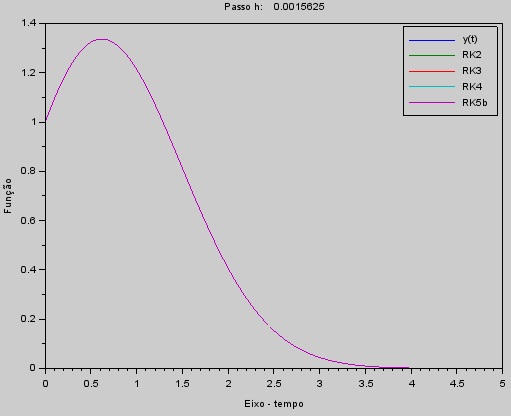 |
| Com um passo $h$ menor, menores os erros de todos os métodos. |
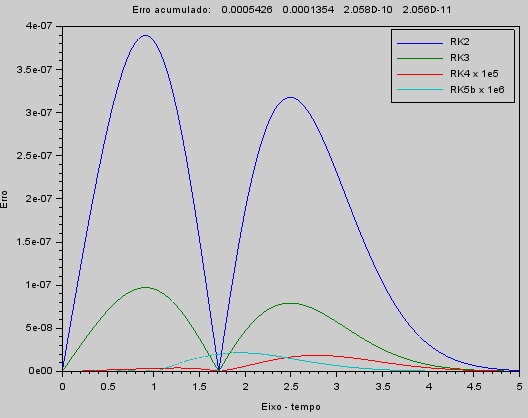 |
| Os métodos de ordem mais alta apresentam uma redução do erro ainda melhor que os métodos de baixa ordem. |
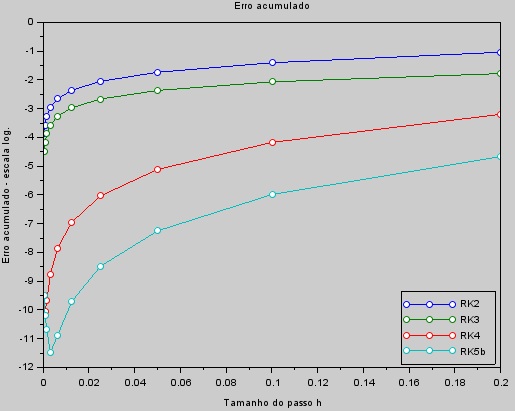 |
| Erro acumulado em função do passo $h$. |
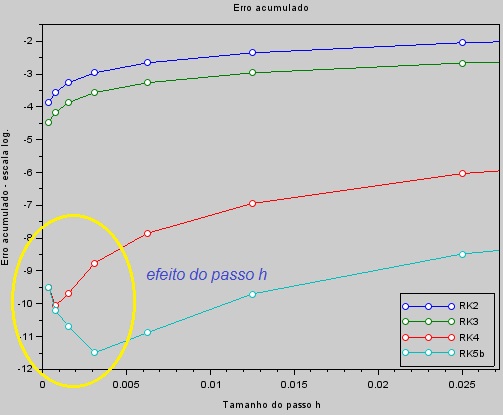 |
| "Zoom" da figura anterior: se o passo for muito pequeno, erros de arrendondamento predominam e diminuem a acurácia. |
Código Scilab:
//// Runge-Kutta: comparações
clc; clear; xdel(winsid()); // limpando e fechando janelas
function f=fd(x, y) //função - EDO
// f = 9.8 - 0.1*y.*y;
f = exp(-x.*x/2) - y.*x;
// f = -y +2*exp(-x).*cos(2*x);
// f = 2*y./(exp(x)+1) + (2.0)./(exp(2*x)+2*exp(x)+1);
// f = -2*y + 2*x.*exp(-2*x);
endfunction
function g=ff(x) //função - solução analítica
k = 7*sqrt(2)/5;
// g = sqrt(98)*(1-exp(-k*x))./(1+exp(-k*x));
g = (x+1).*exp(-x.*x/2);
// g = exp(-x).*sin(2*x);
// g = (exp(x)-1)./(exp(x)+1);
// g = x.*x.*exp(-2*x);
endfunction
h = 0.4; // passo inicial
vh = zeros(10,1); verros = zeros(10,4);
v1 = 1-sqrt(1/2); v2 = 1+sqrt(1/2);
for kh=1:10
h = h/2; vh(kh) = h;
fim = round(5/h);
x0 = 0; y0 = ff(x0); xk = x0;
x = zeros(1,fim); x(1) = x0;
y2 = zeros(1,fim); y2(1) = y0; y2k = y0; // RK-2
y3 = zeros(1,fim); y3(1) = y0; y3k = y0; // RK-3
y4 = zeros(1,fim); y4(1) = y0; y4k = y0; // RK-4
y5b = zeros(1,fim); y5b(1) = y0; y5kb = y0; // RK-5b
for k=2:fim
// RK2:
k1 = h*fd(xk,y2k);
k2 = h*fd(xk+h,y2k+k1);
y2k = y2k + (k1 + k2)/2;
y2(k) = y2k;
// RK3:
k1 = h*fd(xk,y3k);
k2 = h*fd(xk+h/2,y3k+k1/2);
k3 = h*fd(xk+h,y3k+k2);
y3k = y3k + (k1 + 2*k2 + k3)/4;
y3(k) = y3k;
// RK4:
k1 = h*fd(xk,y4k);
k2 = h*fd(xk+h/2,y4k+k1/2);
k3 = h*fd(xk+h/2,y4k+k2/2);
k4 = h*fd(xk+h,y4k+k3);
y4k = y4k + (k1 + 2*(k2 + k3) + k4)/6;
y4(k) = y4k;
// RK5 - Butcher:
k1 = h*fd(xk,y5kb);
k2 = h*fd(xk+h/4,y5kb+k1/4);
k3 = h*fd(xk+h/4,y5kb+(k1+k2)/8);
k4 = h*fd(xk+h/2,y5kb+(k3 - k2/2));
k5 = h*fd(xk+3*h/4,y5kb+(3*k1 + 9*k4)/16);
k6 = h*fd(xk+h,y5kb+(-3*k1+2*k2+12*k3 - 12*k4+8*k5)/7);
y5kb = y5kb + (7*k1 + 32*k3 + 12*k4 + 32*k5 + 7*k6)/90;
y5b(k) = y5kb;
xk = xk + h;
x(k) = xk;
end
ya = ff(x); // função analítica - teórica.
// Erros e somas dos erros absolutos:
e2 = abs(y2-ya); s2 = sum(e2);
e3 = abs(y3-ya); s3 = sum(e3);
e4 = abs(y4-ya); s4 = sum(e4);
e5b = abs(y5b-ya); s5b = sum(e5b);
verros(kh,:) = [s2, s3, s4, s5b];
if kh==1 then // Gráficos:
figure; plot(x,ya,x,y2,x,y3,x,y4,x,y5b);
title(['Passo h: ',string(h)]);
xlabel('Eixo - tempo'); ylabel('Função');
legend('y(t)','RK2','RK3','RK4','RK5b');
figure; plot(x,e2,x,e3,x,e4*100,x,e5b*1e3);
legend('RK2','RK3','RK4 x 100','RK5b x 1e3');
title(['Erro acumulado: ',string([s2, s3, s4, s5b])]);
xlabel('Eixo - tempo'); ylabel('Erro');
end;
if kh==8 then // Gráficos:
figure; plot(x,ya,x,y2,x,y3,x,y4,x,y5b);
title(['Passo h: ',string(h)]);
xlabel('Eixo - tempo'); ylabel('Função');
legend('y(t)','RK2','RK3','RK4','RK5b');
figure; plot(x,e2,x,e3,x,e4*1e5,x,e5b*1e6);
legend('RK2','RK3','RK4 x 1e5','RK5b x 1e6');
title(['Erro acumulado: ',string([s2, s3, s4, s5b])]);
xlabel('Eixo - tempo'); ylabel('Erro');
end;
end;
// Erros em função do passo h:
verros = log10(verros);
figure; plot(vh,verros,'-o');
legend('RK2','RK3','RK4','RK5b',4);
title('Erro acumulado'); xlabel('Tamanho do passo h');
ylabel('Erro acumulado - escala log.');












