Interação predador-presa: resolvendo numericamente o sistema Lotka-Volterra

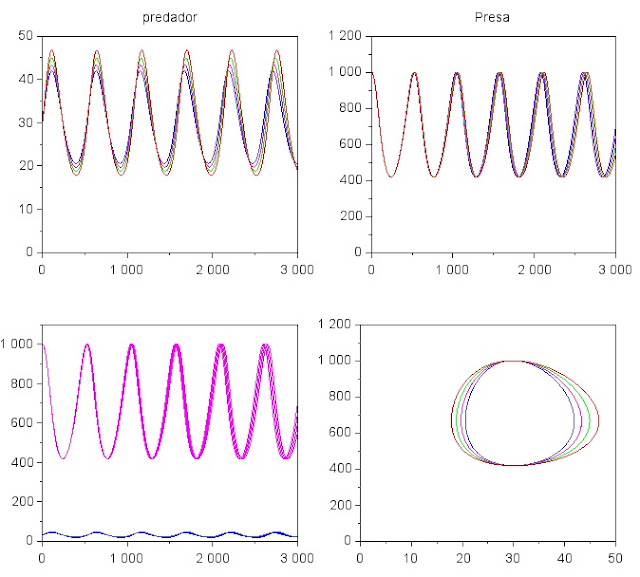
A variação dos parâmetros leva a novas soluções cíclicas.

A convivência entre presas e predadores não é fácil. Os predadores dependem de suas presas para a sobrevivência, as presas, sem esse "controle" externo, poderiam aumentar muito em número e exaurir os recursos, levando toda a população a morrer de fome. É um equilíbrio dinâmico delicado. Esse equilíbrio, para o caso de um predador e uma presa específica, foi matematicamente estabelecido pelos pioneiros na biomatemática A. Lotka e V. Volterra no início do século XX (sim, podemos ter muita matemática até mesmo na biologia).

O sistema de equações diferenciais Lotka-Volterra pode ser expresso por:
$$ \frac{dx}{dt} = x(a - by)$$
$$\frac{dy}{dt} = y(cx - d) $$
Onde $x$ é a população de predadores, $y$ é a população de presas. Pequenas variações nos parâmetros $a$, $b$, $c$ e $d$ podem levar a resultados instáveis e à extinção dos dois grupos. A solução desse sistema de equações (quando não ocorre a extinção) apresenta um comportamento oscilatório periódico simples. Vale lembrar que esse é um modelo muito simples, pois não inclui fatores externos como, por exemplo, o clima, limitação de recursos naturais, competição dentro da própria população, etc.

Por exemplo, se a população de predadores (ex: lobos) for limitada por caçadores humanos sempre que seu número passar de um certo valor, como ficaria solução do sistema? A figura abaixo ilustra essa situação (os predadores são contidos depois do "tempo" 1000 a um valor máximo de 35).

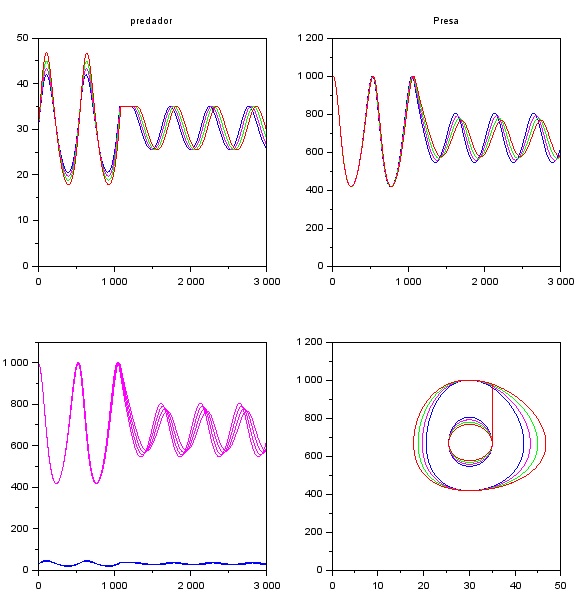Efeito da limitação externa da população de predadores.

O código Scilab abaixo (sem pretensão de ser otimizado) exemplifica a solução numérica do sistema Lotka-Volterra (como de costume - código quase sem comentários).

///// Predador-presa
//  x' = x(-a+by)
//  y' = y(-cx+d)

clc; close; close;
cor = ['b','m','g','r','k','y'];
a = 0.1; b = 0.00015; c = 0.005; d = 0.15;
for r = 1:4
x = 30; 
y = 1000;
vx = [x];
vy = [y];
t = 0; dt = 0.1;
for k=1:2999
    x = x + dt*x*(-a+b*y);
    if k>1000 then if x > 35 then x = 35; end; end;
    y = y + dt*y*(-c*x+d);
    vx = [vx, x];
    vy = [vy, y];
    t = t + dt;
end
subplot(2,2,1); plot(vx,cor(r)); title('predador'); plot([0],[0],'y');
subplot(2,2,2); plot(vy,cor(r)); title('Presa'); plot([0],[0],'y');
subplot(2,2,3); plot(vx,'b'); plot(vy,'m');
subplot(2,2,4); plot(vx,vy,cor(r));  plot([0],[0],'y');
//a = a*0.9; b = b*0.9; 
//c = c*1.1; d = d*1.1;
a = a*1.1; b = b*1.1; 
c = c*0.9; d = d*0.9;
end;