Problema 3n+1 ou Conjectura de Collatz

Fractal Collatz, figura original aqui.

Considere o seguinte algoritmo:

1. escolha um número natural maior que zero;
2. se for um número par, divida-o por dois; se for um número ímpar, multiplique por três e some um;
3. volte ao passo 2.

Como se comporta a sequência numérica assim obtida?

(a) Vai crescer indefinidamente, pois, em média, os números irão crescer a uma taxa 3/2.
(b) Os valores, eventualmente, cairão na sequência 4, 2, 1, 4, 2, 1, 4, 2, 1, ...
(c) Para alguns valores iniciais, o valor final é "infinito", para outros não.
(d) Nenhuma das respostas anteriores.

Ficou na dúvida? Faça um teste, por exemplo, para n = 12. O que acontece? Se você teve paciência suficiente, chegou à conclusão que a resposta correta é o item "b". Pois essa é uma conclusão "precipitada". Ainda não foi rigorosamente provado que, para qualquer número natural, a sequência final será 1, 4, 2, 1, ... Esta é Conjectura de Collatz (ou de Ulam, ou de Thwaites) ou Problema 3n+1 que está em aberto desde 1937. Um problema que pode ser ensinado a uma criança, mas que ainda não foi resolvido. Como Erdos comentou "a matemática ainda não está pronta para este tipo de problema". De qualquer forma, a matemática pode ser bem divertida!

Alguns resultados numéricos:

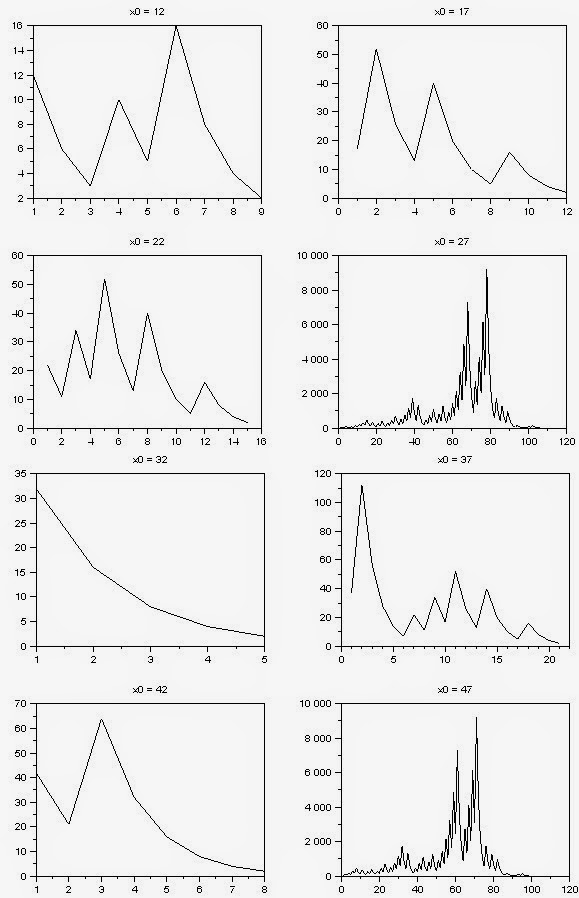A sequência pode varia muito de um número inicial para outro, algumas são curtas outras são bem mais longas.

Valor inicial x tamanho da sequência - grande variação.

Código Scilab:

close; close; close; clc;
p=1;
vtam = [];
for x=5:5:60
    v = [];
    k = 1;
    xk = x+7;
    while xk>1
        v = [v, xk];
        k = k + 1;
        if pmodulo(xk,2) == 0 then
            xk = xk/2;
        else
            xk = xk*3+1;
        end
    end
    subplot(2,2,p); plot(v); title('x0 = '+string(x+7));
    p=p+1;
    vtam = [max(v), vtam]
    if p>4 then
        figure; p=1;
    end
end

xk=5:5:60; xk=xk+7;
figure; plot2d3(xk,vtam);

..............................................

Para saber mais:

• mathworld.wolfram - CollatzProblem.html
• artigo - mbk-78-prev.pdf
• wikipedia.org - Collatz_conjecture