 |
| Figura original aqui. |
A solução numérica de uma equação diferencial (ED) não é uma coisa trivial, mas existem técnicas numéricas já muito bem consolidadas para essa tarefa. Faremos aqui um exemplo mostrando a solução analítica (nem sempre é possível obtermos essa resposta) e a soluções numéricas usando os métodos de Euler (o mais simples) e os métodos de Runge-Kutta de segunda, terceira e quarta ordens (RK2, RK3 e RK4).
Uma equação diferencial pode ser escrita da forma:
E a sua solução usando o método de Euler é dada simplesmente por:
Esse é justamente o Método de Euler. O “passo” Δt precisa ser pequeno e uma condição inicial deve ser conhecida, normalmente em t = 0. Para uma maior precisão nos resultados, entretanto, devemos efetuar mais cálculos (usando, naturalmente, um software + computador).
O método RK2 calcula dois pontos antes de avançar para o ponto seguinte (n+1), da seguinte forma:
De forma semelhante, podemos equacionar o RK3 como:
Finalmente, o RK4:
Contudo, essas expressões são para equações diferenciais de 1o. ordem. A solução numérica de uma equação diferencial de 2a. ordem (ver figura abaixo) requer um pouco mais de astúcia.
O primeiro passo é "quebrar" a ED de 2a. ordem (ver figura acima) em duas de 1a. ordem, formando um sistema com duas de equações. Para isso, precisamos incluir uma nova variável:
Assim, podemos escrever a ED de 2a. ordem como:
Logo, a solução numérica usando o método de Euler pode ser escrita como:
ou, de forma mais compacta:
Devemos lembrar que para resolver uma ED de 2a. ordem precisamos agora de duas condições iniciais, normalmente y(0) e y'(0), ou y(0) e z(0). Seguindo esse raciocínio e usando RK4, podemos escrever a solução numérica de uma solução da ED de 2a. como:
Exemplo usando o Scilab.
No exemplo que segue, resolvemos a seguinte equação diferencial:
Cuja solução analítica é:
Resultados:
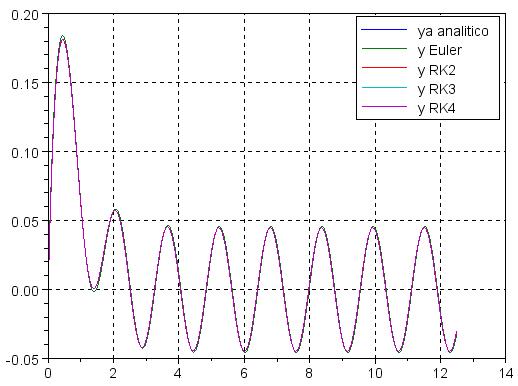 |
| Para este exemplo, os resultados numéricos se aproximam bastante da solução analítica. |
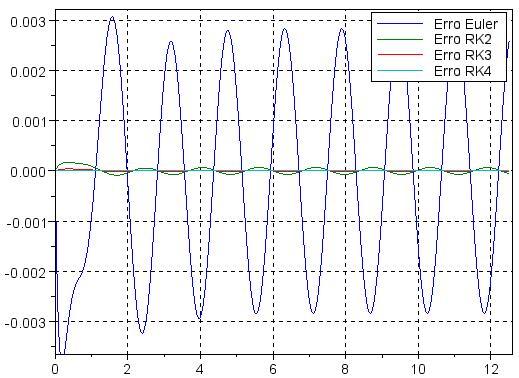 |
| Neste gráfico de erro fica evidente a inferioridade do método de Euler. |
Resultados na forma de tabela de valores:
Valores: ya, y_euler, y_RK2, y_RK3, y_RK4
1.735D-17 0. 0. 0. 0.
0.0237855 0.025 0.02375 0.0237771 0.0237855
0.0452761 0.0474063 0.0452112 0.0452609 0.0452761
0.0646570 0.0674558 0.0645680 0.0646361 0.0646570
0.0820932 0.0853588 0.0819845 0.0820676 0.0820931
0.0977315 0.1013009 0.0976071 0.0977022 0.0977315
0.1117026 0.1154460 0.1115657 0.1116703 0.1117026
0.1241224 0.1279385 0.1239758 0.1240878 0.1241224
0.1350939 0.1389055 0.1349398 0.1350575 0.1350939
0.1447086 0.1484588 0.1445490 0.1446708 0.1447085
0.1530478 0.1566967 0.1528843 0.1530091 0.1530478
0.1601844 0.1637057 0.1600183 0.1601450 0.1601844
0.1661836 0.1695623 0.1660159 0.1661437 0.1661835
0.1711043 0.1743346 0.1709358 0.1710641 0.1711042
0.1750002 0.1780830 0.1748316 0.1749600 0.1750002
Código Scilab:
///////////////////////////////////////////////////////// // Solução numérica de uma equação diferencial de 2a. ordem // usando os métodos de Euler, Runge-Kutta 2, RK3 e RK4 // Eq. dif: y'' + 5y' + 6y = cos(4t) // condições iniciais: y(0)=0 e y'(0)=1 // Solução analítica: // y(t)=0.9*exp(-2*t)-0.88*exp(-3*t)-cos(4*t)/50+2*sin(4*t)/50 ///////////////////////////////////////////////////////// // Prof. Francisco José A. de Aquino // 16 de nov. de 2012 ///////////////////////////////////////////////////////// function fd=ftyz(td, yd, zd) fd = cos(4*td) - 6*yd - 5*zd; endfunction clc; dt = 0.025; t=0:500; t = t*dt; ya = 0.9*exp(-2*t) - 0.88*exp(-3*t) -cos(4*t)/50 + 2*sin(4*t)/50; yn = 0; vy = zeros(1,501); zn = 1; vz = vy; tn = 0; vt = vy; vy(1) = 0; vz(1) = 1; vt(1) = 0; // Euler: for k=2:501 yn = yn + dt*zn; zn = zn + dt*ftyz(tn,yn,zn); tn = tn + dt; vy(k) = yn; vt(k) = tn; end yn = 0; vy4 = zeros(1,501); zn = 1; vz4 = vy4; tn = 0; vt4 = vy4; vy4(1) = 0; vz4(1) = 1; vt4(1) = 0; // RK-4 for k=2:501 k1 = dt*zn; l1 = dt*ftyz(tn,yn,zn); k2 = dt*(zn + l1/2); l2 = dt*ftyz(tn+dt/2,yn+k1/2,zn+l1/2); k3 = dt*(zn + l2/2); l3 = dt*ftyz(tn+dt/2,yn+k2/2,zn+l2/2); k4 = dt*(zn + l3); l4 = dt*ftyz(tn+dt,yn+k3,zn+l3); yn = yn + (k1+2*k2+2*k3+k4)/6; zn = zn + (l1 + 2*l2 + 2*l3 + l4)/6; tn = tn + dt; vy4(k) = yn; vt4(k) = tn; end yn = 0; vy3 = zeros(1,501); zn = 1; vz3 = vy3; tn = 0; vt3 = vy3; vy3(1) = 0; vz3(1) = 1; vt3(1) = 0; // RK-3 for k=2:501 p=2; k1 = dt*zn; l1 = dt*ftyz(tn,yn,zn); k2 = dt*(zn + l1/2); l2 = dt*ftyz(tn+dt/2,yn+k1/2,zn+l1/2); k3 = dt*(zn + l2); l3 = dt*ftyz(tn+dt,yn+k2,zn+l2); yn = yn + (k1+p*k2+k3)/(p+2); zn = zn + (l1 + p*l2 + l3)/(p+2); tn = tn + dt; vy3(k) = yn; vt3(k) = tn; end yn = 0; vy2 = zeros(1,501); zn = 1; vz2 = vy2; tn = 0; vt2 = vy2; vy2(1) = 0; vz2(1) = 1; vt2(1) = 0; // RK-2 for k=2:501 k1 = dt*zn; l1 = dt*ftyz(tn,yn,zn); k2 = dt*(zn + l1); l2 = dt*ftyz(tn+dt,yn+k1,zn+l1); yn = yn + (k1+k2)/2; zn = zn + (l1 + l2)/2; tn = tn + dt; vy2(k) = yn; vt2(k) = tn; end close; close; close; plot(t,ya,vt,vy,vt2,vy2,vt3,vy3,vt4,vy4); xgrid; legend('ya analitico','y Euler','y RK2','y RK3','y RK4'); figure; plot(t,ya-vy,t,ya-vy2,t,ya-vy3,t,ya-vy4); legend('Erro Euler','Erro RK2','Erro RK3','Erro RK4'); xgrid; // Erros: e1m = (abs(ya-vy)); e4m = (abs(ya-vy4)); e3m = (abs(ya-vy3)); e2m = (abs(ya-vy2)); disp([mean(e1m), mean(e2m), mean(e3m), mean(e4m)]); nf = 15; disp('Valores: ya, y_euler, y_RK2, y_RK3, y_RK4'); disp([ya(1:nf)',vy(1:nf)',vy2(1:nf)',vy3(1:nf)',vy4(1:nf)']);
Para saber mais, ver, por exemplo, apostila de Giovani Baratto.




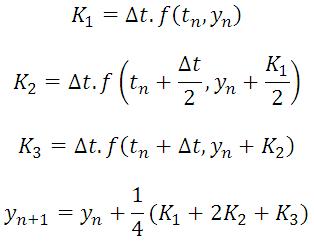


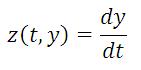




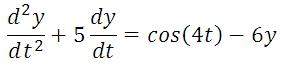

Nenhum comentário:
Postar um comentário